Комбинаторика. Комбинаторные задачи. На завтрак вова может выбрать плюшку бутерброд
Комбинаторика. Комбинаторные задачи.

Муниципальное общеобразовательное учреждение средняя общеобразовательная школа №2 муниципального образования город Горячий Ключ
Урок по теме:
Учитель математики
Минасян Людмила Григорьевна
МБОУ СОШ №2 г.Горячий Ключ
Цель урока: познакомить учащихся с разделом математики – комбинаторикой. Показать решение некоторых комбинаторных задач.
Ход урока: а) объяснение материала; б) закрепление материала, решение задач.
В науке и практике часто встречаются задачи, решая которые приходится составлять различные комбинации из конечного числа элементов и подсчитать число комбинаций.
Такие задачи называются комбинаторными задачами, а раздел математики, в котором рассматриваются эти задачи, называется комбинаторикой.
Слово «комбинаторика» происходит от латинского слова combinate, которое означает «соединять», «сочетать».
Рассмотрим такой
Пример1.
На завтрак Вова может выбрать плюшку, бутерброд, пряник или кекс, а запить их он может кофе, соком или кефиром.
Из скольких вариантов завтрака Вова может выбирать?
Решение.
| Плюшка | Бутерброд | Пряник | Кекс | |
| Кофе | Кофе Плюшка | Кофе Бутерброд | Кофе Пряник | Кофе Кекс |
| Сок | Сок Плюшка | Сок Бутерброд | Сок Пряник | Сок Кекс |
| Кефир | Кефир Плюшка | Кефир Бутерброд | Кефир Пряник | Кефир Кекс |
Всего вариантов столько же, сколько клеток в таблице.
Ответ: 12.
Однако составлять такие таблицы для каждой задачи, занимает время.
А чтобы решить такую задачу быстрее, можно воспользоваться правилом умножения.
Правило умножения.
Для того, чтобы найти число всех возможных исходов независимого проведения двух испытаний А и В , следует перемножить число всех исходов испытания А и число всех исходов испытания В.
Пример 2.
Несколько стран в качестве символа своего государства решили использовать флаг в виде трех горизонтальных полос одинаковых по ширине, но разных по цвету: белый, синий, красный.
Сколько стран могут использовать такую символику при условии, что у каждой страны свой, отличный от других, флаг?
Решение будем искать с помощью «дерева возможных вариантов».
Посмотрим на левую «веточку», идущую от «флага», пусть верхняя полоса – белого цвета, тогда средняя полоса может быть синей или красной, а нижняя – соответственно, красной или синей. Получилось два варианта цветов полос флага: белая, синяя, красная и белая, красная, синяя.
Пусть теперь верхняя полоса – синего цвета, это вторая «веточка».
Тогда средняя полоса может быть белой или красной, а нижняя - соответственно, красной или белой. Получилось еще два варианта цветов полос: синяя, белая, красная и синяя, красная, белая.
Аналогично рассматривается случай для верхней полосы красного цвета.
Получается еще два варианта: красная, белая, синяя и красная, синяя, белая.
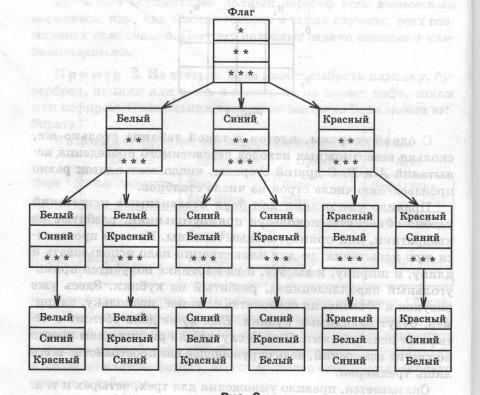
Всего 6 комбинаций.
Ответ: 6.
Построенная схема действительно напоминает дерево, только перевернутое. Поэтому ее называют «деревом возможных вариантов».
А вот так выглядит «дерево возможных вариантов» для такого примера 3:
studfiles.net
Перебор возможных вариантов

Разделы: Математика, Конкурс «Презентация к уроку»
Презентация к уроку
Загрузить презентацию (586,8 кБ)
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Цели урока:
Образовательная:
- Формирование опорной системы знанийпо теме.
Развивающие
- Развитие логического мышления при анализе нового материала.
- Формирование интеллектуальных умений (овладение мыслительными операциями анализа, сравнения, обобщения и т.д.)
Воспитательная
- Создание дидактических условий для обеспечения положительного эмоционального процесса обучения:
- привлечение яркого фактического материала,
- опора на явление окружающей жизни и опыт учащихся,
- побуждение их к оценке и выражению собственного отношения к изучаемым явлениям.
Программное обеспечение: мультимедийный проектор, компьютер, интерактивная доска.
Методическое обеспечение: презентация.
План урока:
- Организационный момент – 1 мин.;
- Устная работа – 3 мин.;
- Изучение нового материала – 7-8 мин.;
- Формирование умений и навыков – 26-30 мин.;
- Итоги урока – 1-2 мин.;
- Домашнее задание – 1-2 мин.
Ход урока
I. Организационный момент
II. Устная работа
Вычисли устно: (слайд 3)

III. Изучение нового материала
Перед нами нередко возникают проблемы, которые имеют не одно, а несколько различных решений. Обычно одни из них нас устраивают, а другие нет.
Рассмотрим первый пример:
1. Сколько двузначных чисел можно составить из цифр 1, 4 и 7? (слайд 4)
Решение на доске учителем и учащимися.
| 1 | 4 | 7 | |
| 1 | 11 | 14 | 17 |
| 4 | 41 | 44 | 47 |
| 7 | 71 | 74 | 77 |
Перебором:
Ответ: 9 чисел.
2. Сколько чётных двузначных чисел можно составить из цифр 0, 1, 2, 4, 5, 9? (слайд 5)
Учитель обращает внимание на способ оформления решения с помощью таблицы. Учащимся предлагается найти сходство и различия в задачах №1 и №2.
После обсуждения строится таблица.
| 0 | 2 | 4 | |
| 1 | 10 | 12 | 14 |
| 2 | 20 | 22 | 24 |
| 4 | 40 | 42 | 44 |
| 5 | 50 | 52 | 54 |
| 9 | 90 | 92 | 94 |
5 * 3 = 15 чётных двузначных чисел
3. В алфавите племени УАУА имеются только две буквы – «а» и «у». Сколько различных слов по три буквы в каждом слове можно составить, используя алфавит этого племени?
Учитель предлагает решить учащимся самостоятельно, с проверкой на доске.
4. На завтрак Вова может выбрать плюшку, бутерброд, пряник или кекс, а запить их он может кофе, соком или кефиром. Из скольких вариантов завтрака Вова может выбрать?
Учащиеся решают вместе с учителем ( слайд 6)
| Плюшка | Бутерброд | Пряник | Кекс | |
| Кофе | Плюшка Кофе | Бутерброд Кофе | Пряник Кофе | |
| Сок | Плюшка Сок | Бутерброд Сок | Пряник Сок | Кекс Сок |
| Кефир | Плюшка Кефир | Бутерброд Кефир | Пряник Кефир | Кекс Кефир |
3 * 4 = 12 – вариантов завтрака
Выводы:
В данных примерах был осуществлен способ перебора возможных вариантов (возможных комбинаций). Поэтому данные задачи называют комбинаторными. Решения данных задач основывается на общем правиле умножения. (слайд 7)
"Правило умножения"
Для того чтобы найти число всех возможных исходов независимого проведения двух испытаний А и В, следует перемножить число всех исходов испытания А и число всех исходов испытания В
IV. Формирование умений и навыков
Реши самостоятельно (слайд 8)
-
Составьте все двузначные числа, в записи которых используются только цифры 3 и 7.
-
Сколько двузначных чисел можно составить, в записи которых используются цифры 2, 4, 7, 8? Сколько двузначных чисел можно записать, если использовать при записи числа каждую из указанных цифр только один раз? Сколько чётных двузначных чисел получится из этих цифр?
-
Сколькими способами можно составить патруль из двух милиционеров, если на дежурство вышли четверо: Быков, Свистунов, Умнов и Дубов?
-
В четверг в первом классе должно быть три урока: русский язык, математика и физкультура. Сколько различных вариантов расписания можно составить на этот день?Указание: перебирая варианты, введите обозначения: Р – русский язык, М – математика, Ф – физкультура.
(Решение задач самостоятельное, с последующей проверкой на доске (слайды 9,10))
V. Итоги урока
выставление оценок.
VI. Домашнее задание
(слайд 11)
1. Сколько можно составить двузначных чисел, в записи которых используются только цифры 1, 5, 6, 8? Сколько двузначных чисел можно записать, если использовать при записи числа каждую из указанных цифр только один раз? Сколько получится чётных чисел? Сколько получится чисел, которые делятся на пять?
2. Сколькими способами можно выбрать два цветка, если есть васильки, маки, тюльпаны и ромашки? Сколько получится таких пар, если их составлять из двух разных цветков?
Используемая литература:
- События. Вероятности. Статистическая обработка данных: Доп. параграфы к курсу алгебры 7-9 кл. общеобразоват. учреждений / А.Г. Мордкович, П.В. Семенов. – 4-е изд. – М.: Мнемозина, 2006.
- Вероятность и статистика. 5-9 кл.: пособие для общеобразоват. учеб. заведений / Е.А. Бунимович, В.А. Булычев. – 2-е изд. стереотип. – М.: Дрофа, 2004.
- Алгебра : элементы статистики и теории вероятностей : учеб. пособие для учащихся 7-9 кл. общеобразоват. учреждений / Ю.Н. Макарычев, Н.Г. Миндюк; под ред. С.А. Теляковского. – 4-е изд. – М.: Просвещение, 2006.
- Бродский И.Л., Литвиненко Р.А. Вероятность и статистика. 7-9 классы. Решение задач из учебника под редакцией Г.В. Дорофеева. – М.: АРКТИ, 2006
- Теория вероятностей и статистика для школьников( задачи и решения)/ Учебно-практическое пособие. Г.И.Просветов.- Москва:Альфа-Пресс, 2009.
xn--i1abbnckbmcl9fb.xn--p1ai
Денежно-вещевая лотерея в выборе не участвует, поэтому

Задача 8.Сколько имеется путей, которыми
можно попасть из города А в город С
через город В, если из А в В ведут две дороги,
а из В и С – три дороги?

Задача 9.На книжной полке стоят 25 книг по математике,
15 – по физике,
10 – по астрономии. Сколькими способами можно выбрать
3 книги так, чтобы одна книга была по математике, другая – по физике
и третья – по астрономии?

Решение.
Составим таблицу: слева от первого столбца – первые цифры искомых чисел, а выше первой строки – вторые цифры этих чисел (учитывая, что числа – четные, т.е. оканчиваются на 0,2,4).
| 0 | 2 | 4 |
1 | 10 | 12 | 14 |
2 | 20 | 22 | 24 |
4 | 40 | 42 | 44 |
5 | 50 | 52 | 54 |
9 | 90 | 92 | 94 |
5 строк · 3 столбика = 15 чисел Ответ: 15.

Задача 11.Сколько двузначных чисел можно составить, используя цифры 1,4,7, если цифры в числе не повторяются?

Решение.
При использовании правила умножения применяют схему – дерево возможных вариантов.
Двузначное число
1 цифра числа
2 цифра числа
4 7 1 7 1 4
14,17 41,47 71,74

Задача 12.На завтрак Вова может выбрать плюшку, бутерброд, пряник или кекс, а запить их он может кофе, соком или
кефиром.
Из скольких вариантов завтрака Вова может выбирать?
studfiles.net